CS 570CS570 Midterm Exam 3 Spring2015 solutions Analysis of Algorithms Spring LATEST UPDATE Exam III

Document Content and Description Below

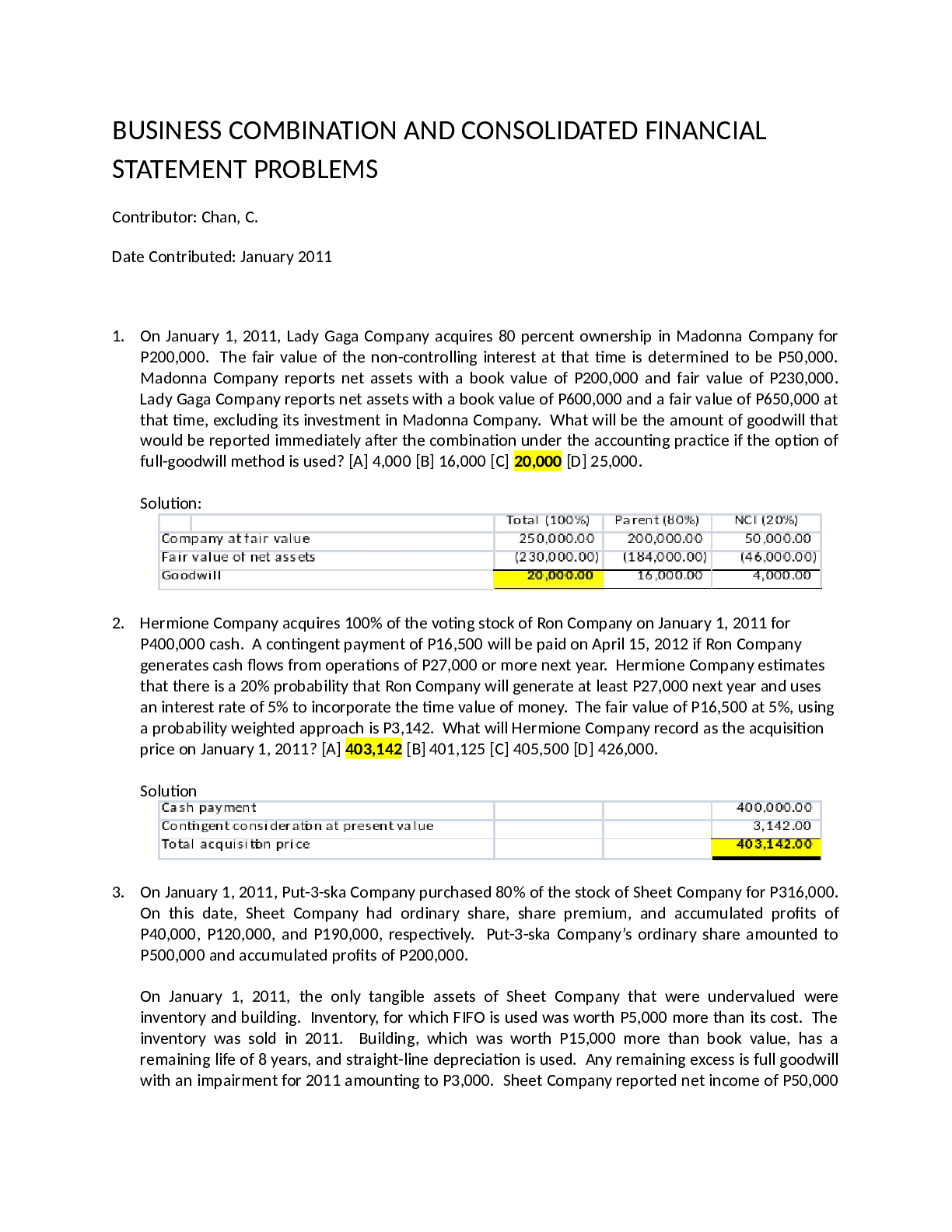
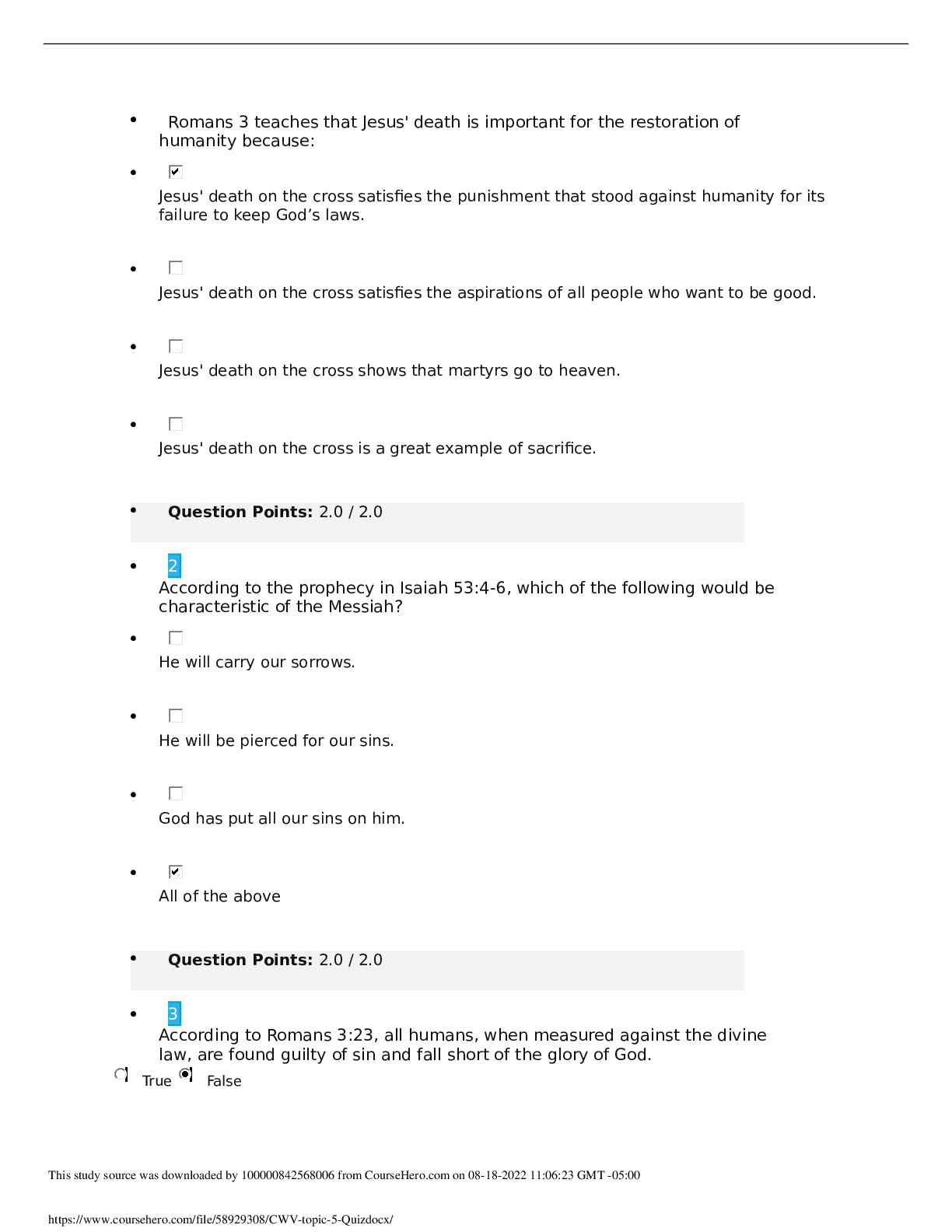
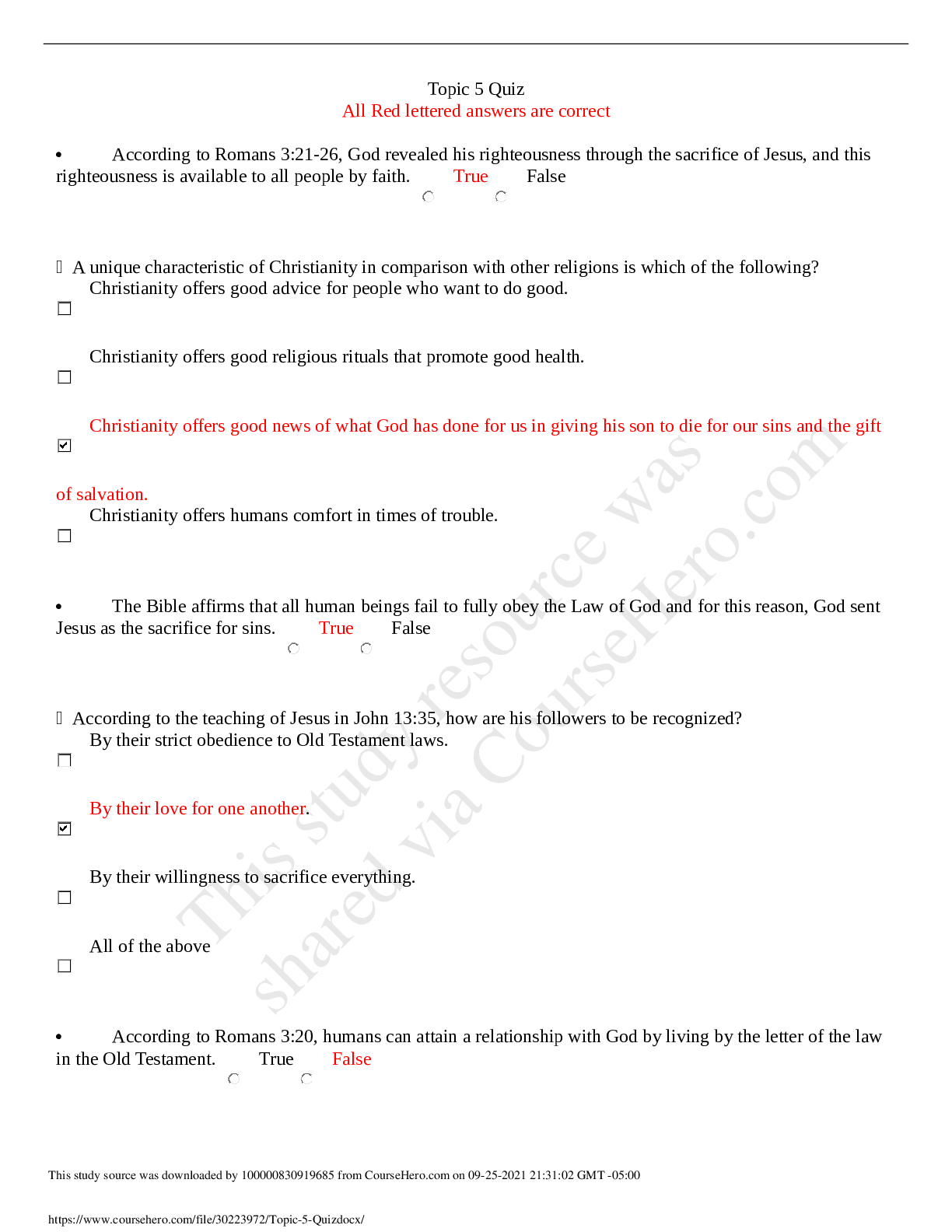
CS570 Analysis of Algorithms Spring 2015 Exam III Name: _____________________ Student ID: _________________ Email Address:_______________ _____Check if DEN Student Maximum Received Problem 1 ... 20 Problem 2 16 Problem 3 16 Problem 4 16 Problem 5 16 Problem 6 16 Total 100 Instructions: 1. This is a 2-hr exam. Closed book and notes 2. If a description to an algorithm or a proof is required please limit your description or proof to within 150 words, preferably not exceeding the space allotted for that question. 3. No space other than the pages in the exam booklet will be scanned for grading. 4. If you require an additional page for a question, you can use the extra page provided within this booklet. However please indicate clearly that you are continuing the solution on the additional page.1) 20 pts Mark the following statements as TRUE or FALSE. No need to provide any justification. [ TRUE ] If SAT ≤P A, then A is NP-hard. [FALSE ] If a problem X can be reduced to a known NP-hard problem, then X must be NPhard. [ TRUE] If P equals NP, then NP equals NP-complete. [FALSE ] Let X be a decision problem. If we prove that X is in the class NP and give a polytime reduction from X to Hamiltonian Cycle, we can conclude that X is NP-complete. [ TRUE] The recurrence T (n )=2T (n/2)+3n , has solution T (n )=θ(nlog (n2)). [ FALSE ] On a connected, directed graph with only positive edge weights, Bellman-Ford runs asymptotically as fast as Dijkstra. [ TRUE] Linear programming is at least as hard as the Max Flow problem in a flow network. [ TRUE] If you are given a maximum s-t flow in a graph then you can find a minimum s-t cut in time O(m) where m is the number of the edges in the graph. [ TRUE] Fibonacci heaps can be used to make Dijkstra’s algorithm run in O( |E| + |V| log|V| ) time on a graph G=(V,E) [Show More]

Last updated: 1 year ago

Preview 1 out of 10 pages